Radix sort란 가장 낮은 자릿수부터 해서 정렬해나간다는 원리이다. 다른정렬과 다르게 별도로 비교연산이 없고,
따라서 시간복잡도는 굉장히 빠른 O(N)이다.
최대자릿수 까지 N번 탐색을 한다고 하면
즉, 10개의 값이 있고 최대자릿수가 3이라고 가정했을 때
일의 자릿수를 찾는 과정에서 = 10번 탐색
십의 자릿수를 찾는 과정에서 = 10번 탐색
백의 자릿수를 찾는 과정에서 = 10번 탐색
즉 3 x 10 번 탐색을 하게된다. 이를 식으로 써보면 K * N번 탐색을 하는 것이고 이를 빅오 표기법으로 나타내면 O(KN)이 된다.
하지만 자릿수마다 정렬을 하기때문에 정렬된 수를 큐에 담고 또 빼내는 과정해서 추가적인 메모리소요가 많다.
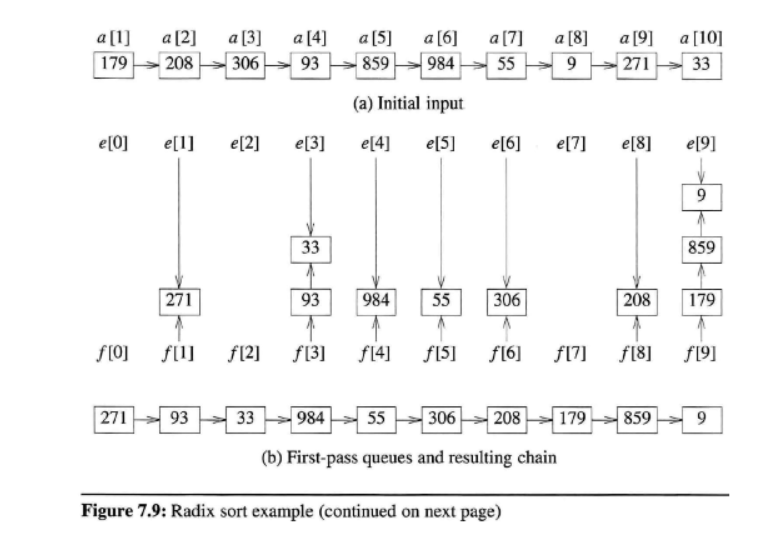
본래있던 기수정렬의 출력방식을 조금 응용해서 link를 통한 출력방식을 사용하였다.
원래는 자릿수에 맞는 인덱스의 큐에 들어가서 뺴낼때 하나씩 빼내는것이 본래였다면, link를 통해 간단히 다음큐의 front만 가리킨다면, 쉽게 출력을 할 수 있을 것이다.
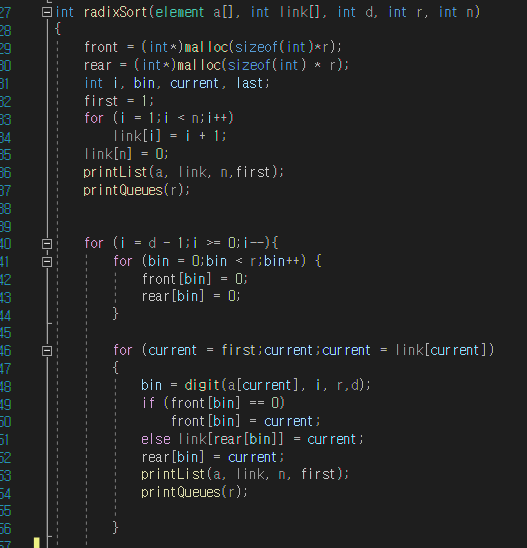
윗부분에선 먼저 링크배열은 바로다음인덱스를 가리키도록 초기화시키고,
digit 함수로 끝자리를 검사해 bin에 담아 bin 인덱스의 큐에 삽입한다.
큐는 rear와 front만 존재하게 되는데, 같은 자릿수가 2개이상 들어올 경우 그 사이의 링크는 link[rear[bin]] = current를 통해 링크함수로 이어놓는다. 따라서 큐는 front와 rear 둘의 성분만 가지고있어도 된다.

digit은 자릿수에 맞는 값을 반환해준다.

이 코드부분은 실질적으로 link배열을 통해 큐안에서 rear와 다음인덱스 front를 이어주는 역할을 한다.

<참고>
06 정렬 알고리즘 - 기수 정렬(Radix Sort)
기수정렬 (Radix Sort) 기수정렬은 낮은 자리수부터 비교하여 정렬해 간다는 것을 기본 개념으로 하는 정렬 알고리즘입니다. 기수정렬은 비교 연산을 하지 않으며 정렬 속도가 빠르지만 데이터 전�
lktprogrammer.tistory.com
'Data Structure' 카테고리의 다른 글
| 해쉬(Hash) (0) | 2020.06.16 |
|---|---|
| 힙 정렬(Heap sort) (0) | 2020.06.15 |
| 합병정렬(Merge sort) (0) | 2020.06.15 |
| 퀵 정렬(Quick Sort) (0) | 2020.06.15 |
| 정렬 - 삽입정렬(insortion sort) (0) | 2020.06.15 |
